Aquí os dejo los vídeo con un curso sobre convergencia y divergencia de integrales impropias
Separar y clasificar integrales impropias: ver Video
Primero hay que estudiar la continuidad de la función y mirar si tiene algún intervalo al infinito, y separar la integral para poder estudiar cada tipo de discontinuidad o intervalo al infinito por separado.

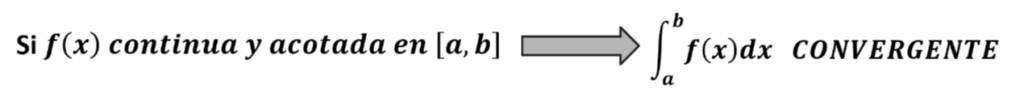
Si la función es continua y acotada es convergente y ya hemos acabado.
Si la función no es continua y acotada seguiremos su estudio.
En el caso de que sean integrales de primera especie (intervalo a infinito), antes de mirar ningún criterio de convergencia tendremos que hacer el límite al infinito.

A partir de aquí ya podemos aplicar criterios de convergencia.
Criterios de Convergencia Integral p: ver Video
Este es el criterio de convergencia que se utiliza más, aunque no tengamos funciones tan sencillas en la mayoría de los casos compararemos con una función del tipo 1/x^p ..
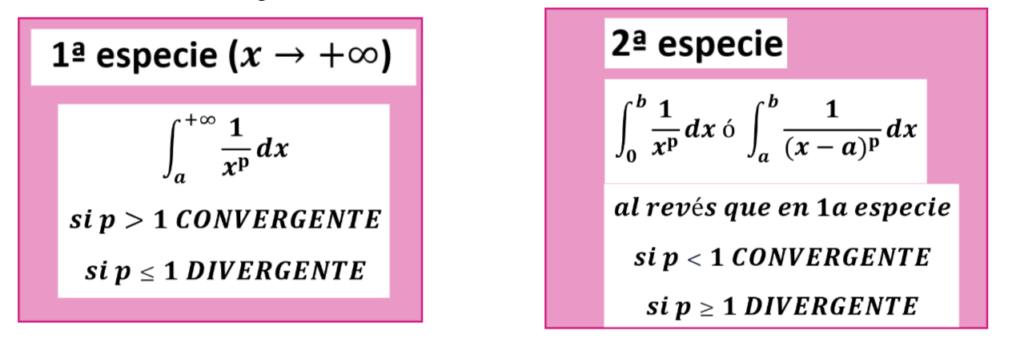
Lo mejor es aprenderse el de primera especie y recordar que el segunda especie va al revés.
Haremos los siguientes ejemplos:
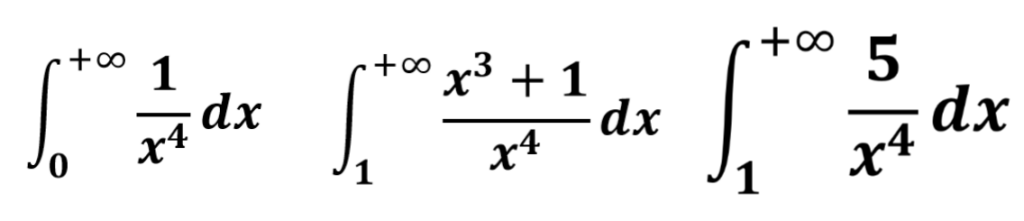
Una vez conocemos el criterio de convergencia de las funciones del tipo 1/x^p , ya podemos empezar a comparar funciones.
Hay dos maneras de compara funciones: comparación directa o con el límite (funciones con el mismo caracter).
Comparación directa de integrales impropias: ver Video
Intentaremos encontrar funciones que sean mayores o menores que las que tenemos.
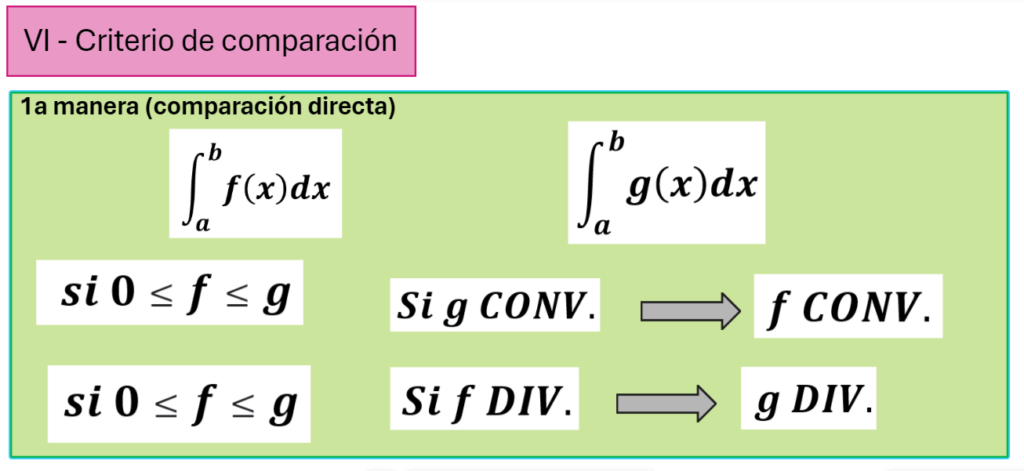
Haremos los siguientes ejemplos:
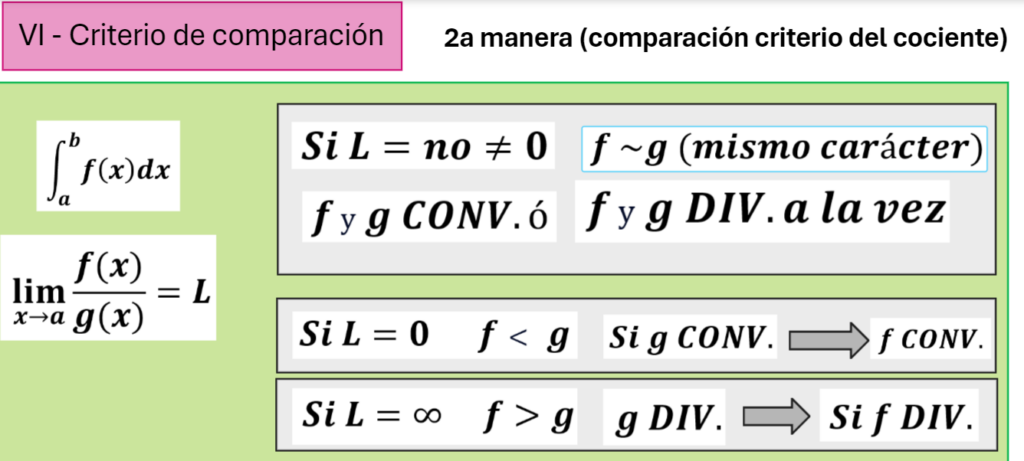
Comparación mediante el límite de integrales impropias: ver Video
Intentaremos encontrar funciones que tengan el mismo carácter que la que tenemos. Una función con el mismo carácter es un función que se comporta de la misma manera que otra donde la estamos estudiando.
Si no podemos encontrar una función con el mismo carácter, buscaremos funciones que sean mayores o menores.
Podremos comprobar que hemos escogido la función correcta, haciendo el límite de una función entre la otra.
haremos los siguientes ejemplos:
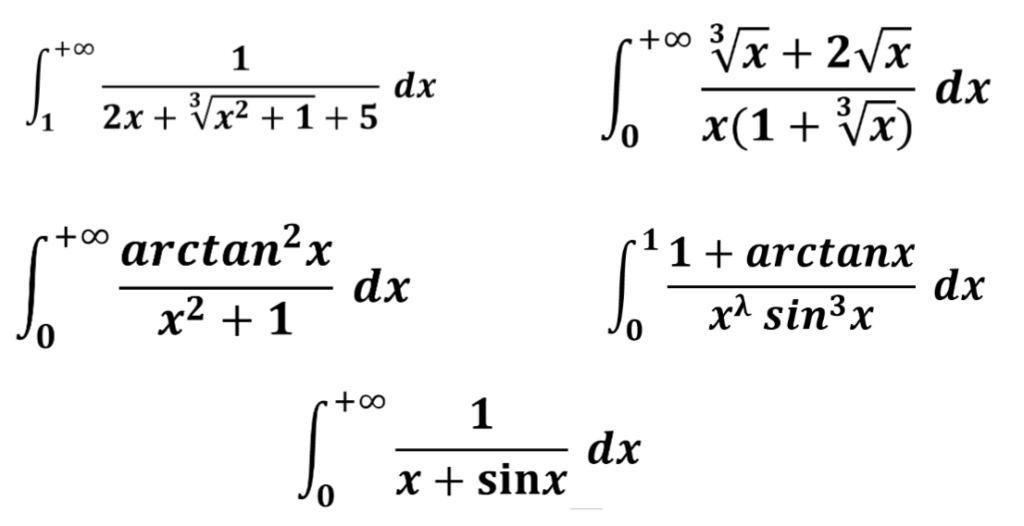
A partir de aquí, veremos como estudiar la convergencia de algunas funciones: senos y cosenos, exponencial y logaritmos.
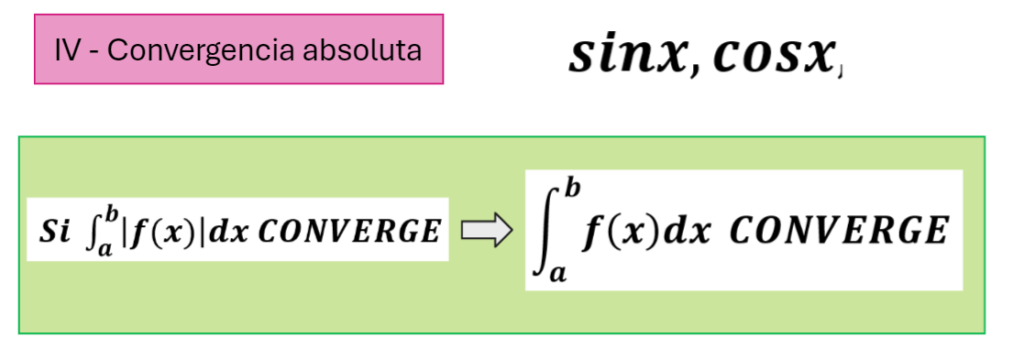
Criterio de la Convergencia Absoluta (Senos y Cosenos): ver Video
Cuando aparecen senos y cosenos en integrales convergentes al infinito (1a especie), a veces es imposible encontrar una función que tenga el mismo carácter (que se comporte de la misma manera). Tendremos que recurrir a aplicar el criterio de la convergencia absoluta:
Haremos 3 ejercicios resueltos:
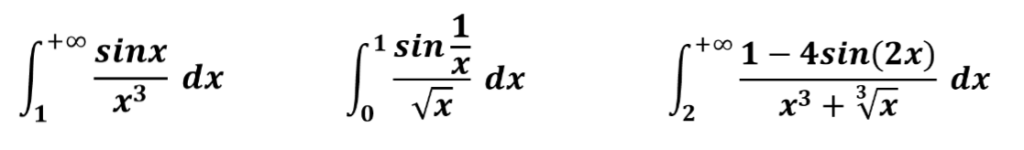
Criterio de Convergencia del número e (Función Gamma)(Exponencial): ver Video
Cuando aparece la función exponencial (número e), gracias a la función Gamma, podemos comparar la función con una función del tipo 1/x^n .
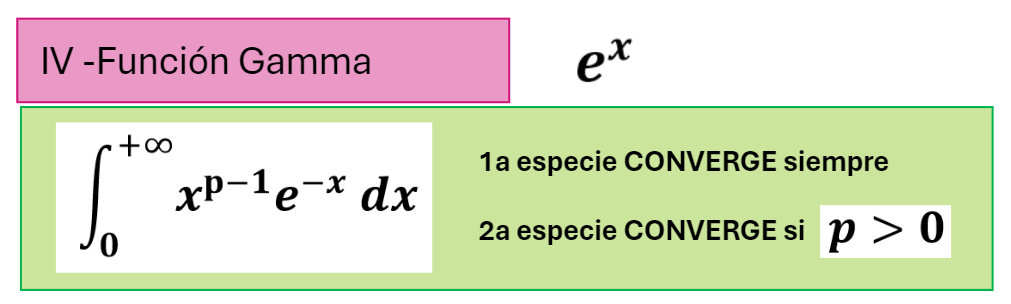
No hace falta que nos aprendamos cuando converge la función Gamma. Haremos el siguiente ejemplo de integral de tercera especie.
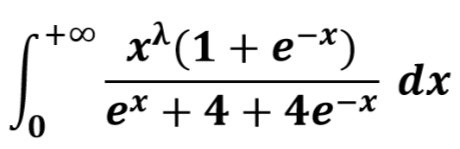
Convergencia de integrales impropias Logaritmos: ver Video
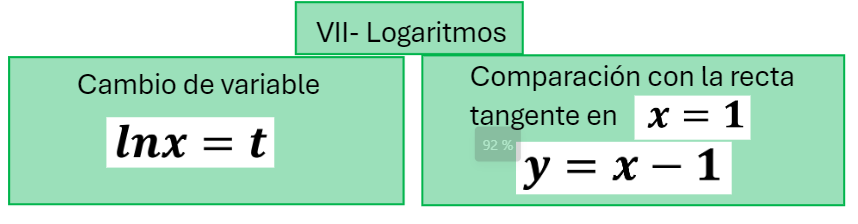
Podemos estudiar la convergencia de una integral impropia cuando aparecen logaritmos neperianios de varias maneras. En el vídeo usamos dos:
- Cambio de variable
- Comparando el logaritmo con su recta tangente en x=1
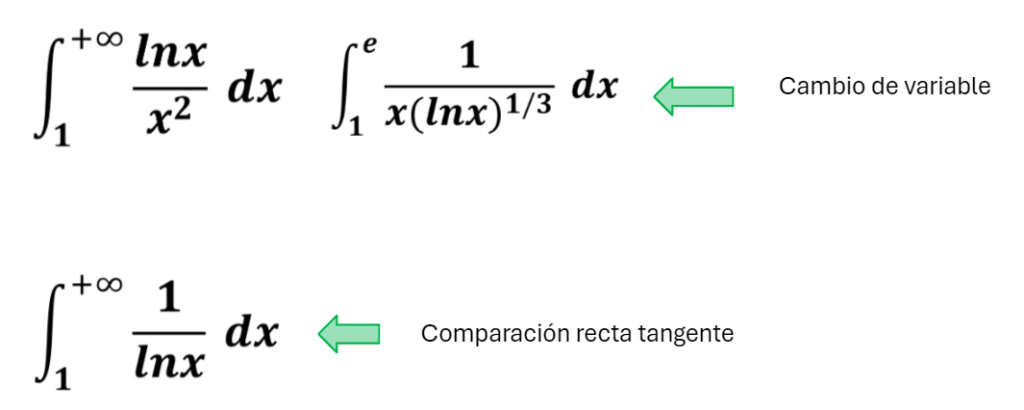
Haremos los siguientes ejercicios resueltos:
Visita mi canal de YouTube: @ProfeInDaHouse
