Máximos relativos, mínimos relativos y Puntos de Silla
Buscaremos:
- máximos relativos, mínimos relativos y puntos de silla de 2 variables
- máximos relativos, mínimos relativos y puntos de silla de 3 variables
- máximos y mínimos restringidos en un entorno = máximos y mínimos absolutos de varias variables con 2 métodos:
- Método de los Multiplicadores de Lagrange
- Directamente trabajando sobre la región
Máximos relativos, mínimos relativos y Puntos de Silla (desde cero) ver Video
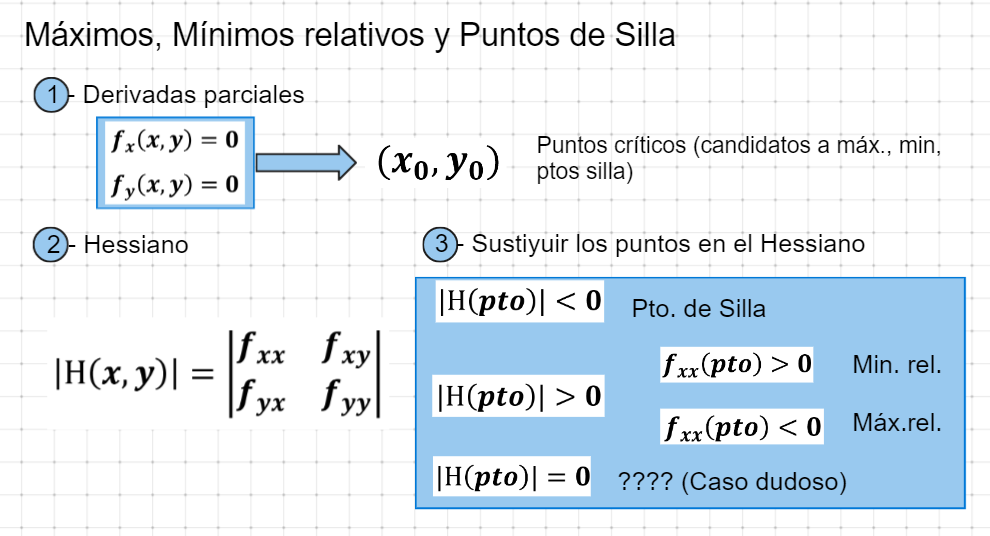
Para encontrar los puntos críticos (es decir máximos y mínimos relativos y puntos de silla) podemos seguir el siguiente esquema (2 variables):
En el video veremos el siguiente ejemplo:
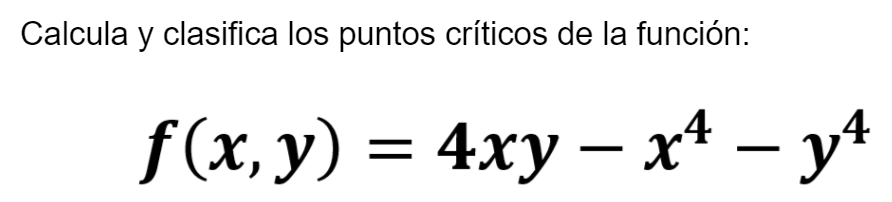
Máximos relativos, mínimos relativos y Puntos de Silla de 3 Variables ver Video
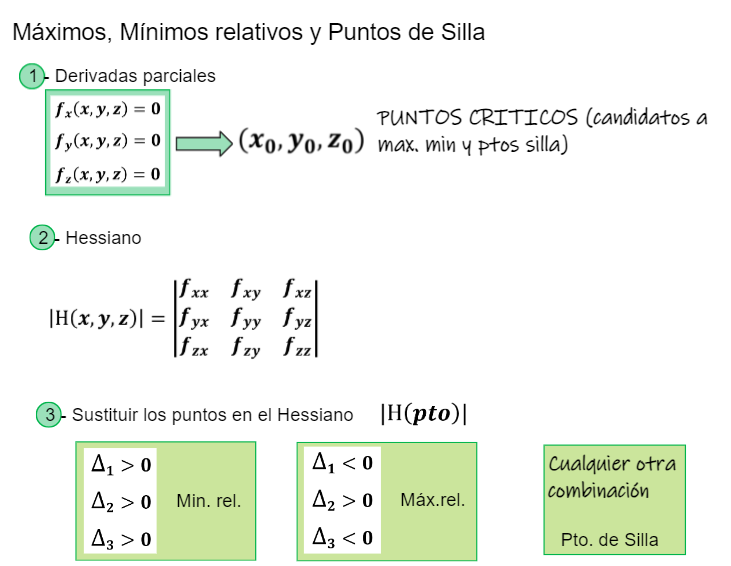
Para encontrar los puntos críticos de una función de 3 variables, podemos seguir el siguiente esquema:
En el vídeo haremos el siguiente ejemplo:

Extremos absolutos condicionados a una restricción:
Si nos dan una función restringida dentro de un entorno, además de calcular los máximos, mínimos relativos y puntos de silla de dentro del recinto, también tendremos que encontrar los máximos y mínimos sobre la restricción. Podemos hacerlo de 2 maneras: con los Multiplicadores de Lagrange o directamente sobre la restricción.
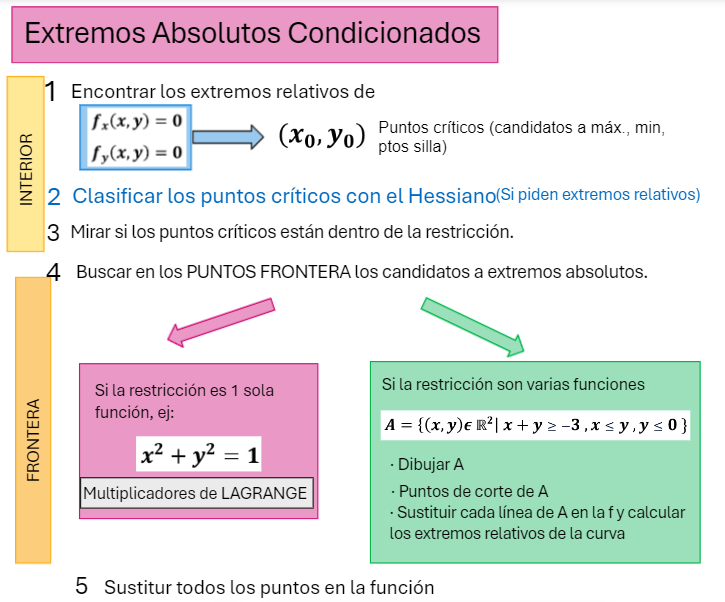
Multiplicadores de Lagrange
Máximos y Mínimos restringidos por Multiplicadores de Lagrange: ver Video
Haremos el siguiente ejercicio resuelto, mediante el método de los Multiplicadores de Lagrange:

Extremos Absolutos de una función de dos variables (Extremos Condicionados) ver Video
Haremos el siguiente ejercicio resuelto:

Visita mi canal de YouTube: @ProfeInDaHouse
