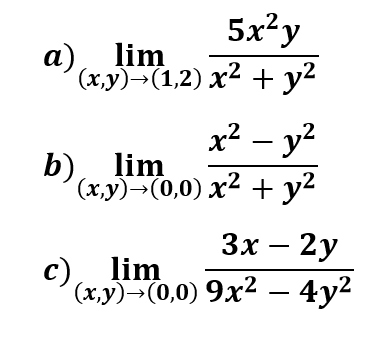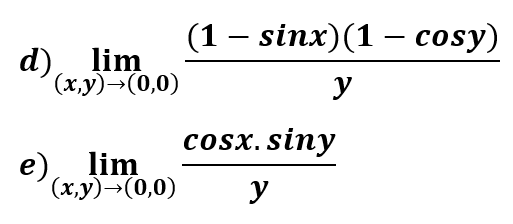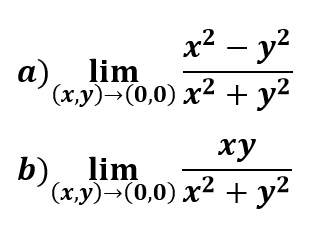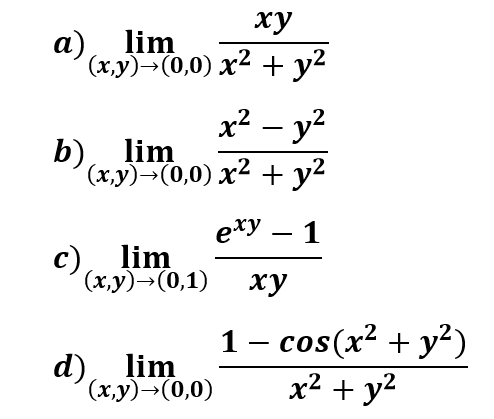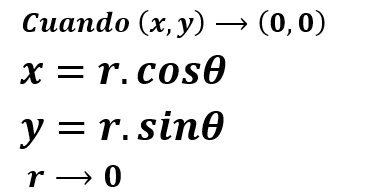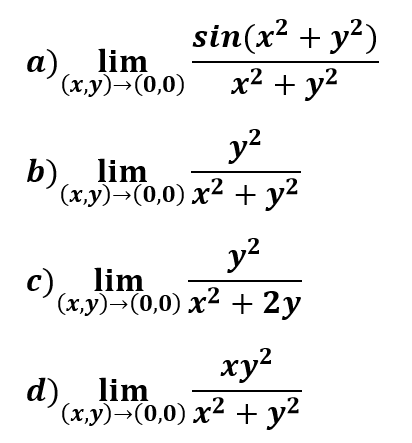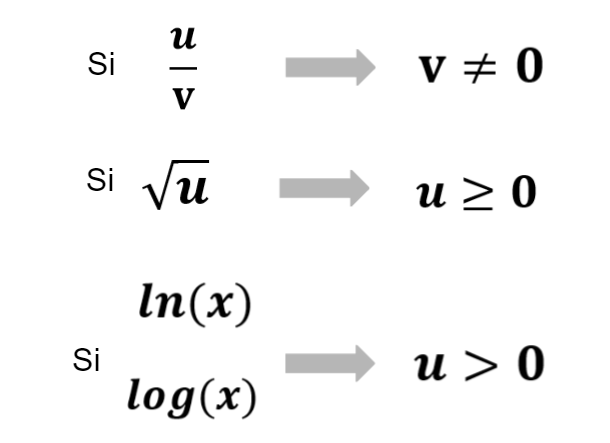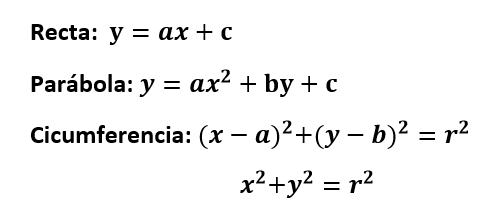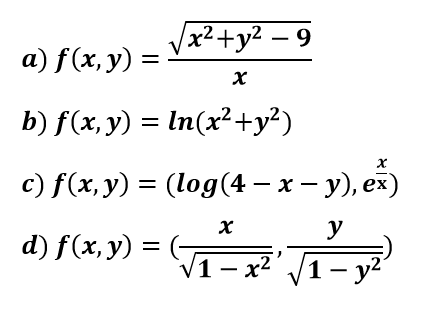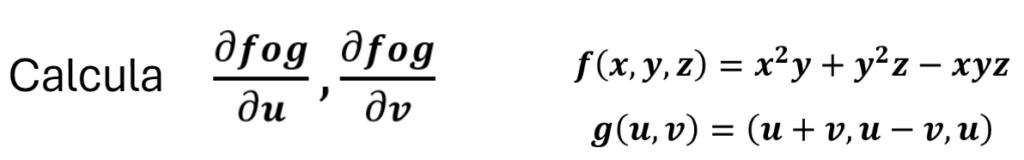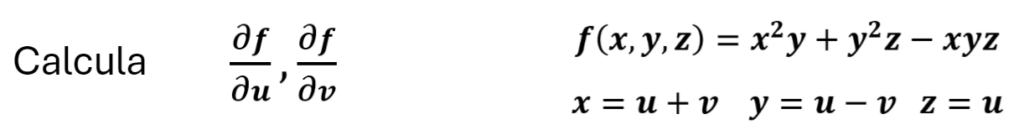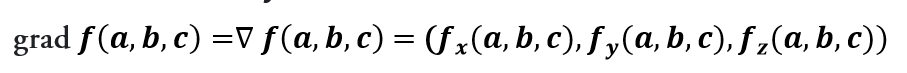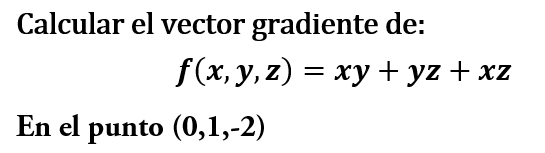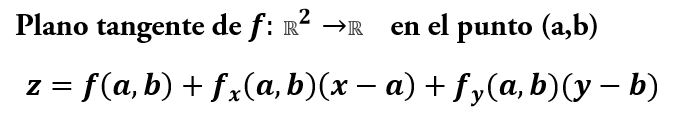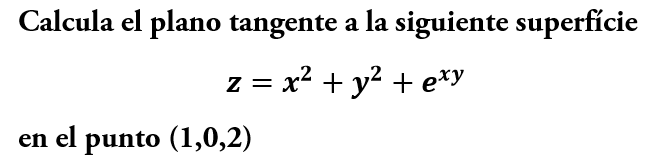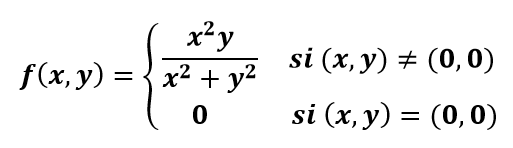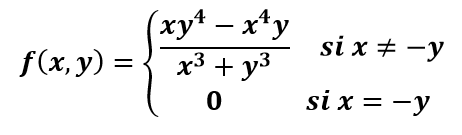Ejercicios Resueltos de Funciones de Varias Variables
Cálculo Multivariable Aquí os dejo vídeos con ejercicios resueltos:
Como encontrar y representar el Dominio: Vídeo con 3 ejemplos El dominio de una función son los valores de las funciones de entrada para los que existe la función.
Como pasaba en las funciones de una variable tendremos que tener en cuenta:
Las funciones más habituales que nos vamos a encontrar y que tendremos que conocer para encontrar el dominio o dibujar la curva de nivel son:
Encontraremos el dominio de estos cuatro ejemplos:
Dentro de este apartado haremos ejemplos de los siguientes tipos de límites de funciones de varias variables:
Límites directos y por factorización Límites iterados o reiterados Límites direccionales o por trayectorias Límites por cambio a coordenadas polares
Derivadas Parciales: Ejemplo 1 de derivadas parciales: ver Video
Ejemplo 2 de derivadas parciales : ver Video
Ejemplo 3 de derivadas parciales : ver Video Derivadas parciales por Derivación Implícita: Ejemplo 1 de derivadas parciales desde cero: ver Video Ejemplo 2 de derivadas parciales: ver Video
Calcularemos las derivadas parciales de una función de varias variables utilizando la regla de la cadena, es decir que aplicaremos la regla de la cadena a una función compuesta .
Haremos este ejemplo:
Ese mismo ejemplo, preguntado de otra manera:
Ejercicio resuelto de regla de la cadena: ver Video El vector gradiente en un punto, es el vector que contiene las derivadas parciales en ese punto:
haremos el siguiente ejemplo:
Como calcular el plano tangente de una función de dos variables: (2 métodos)Podemos calcular el plano tangente de dos formas según si la función que nos dan está definida explícitamente (la z despejada) o implícitamente :
El plano tangente de una función de varias variables en un punto es:
Veremos como se calcula y haremos el siguiente ejercicio:
El método anterior NO lo podremos hacer siempre, el siguiente método sirve para calcular el plano tangente de cualquier función de 2 variables:
Si la función está definida implícitamente, tendremos que calcular el plano tangente multiplicando por el gradiente:
Haremos el siguiente ejercicio resuelto:
En este apartado veremos 3 métodos resueltos de como calcular la derivada direccional:
(con la fórmula ) derivada direccional de una función en un punto según la dirección de un vector
derivada direccional máxima en un puntoderivadas direccionales por la definición
Derivadas parciales por la definición
En las funciones definidas a trozos , en los puntos en los que se separa la función, estamos obligados a usar la definición de derivada parcial .
a) Haremos dos ejemplos usando la definición de derivada parcial en un punto. En el primer ejercicio la función se separa en un punto:
b) En el segundo ejercicio resuelto, la función se separa en otra función (una recta):
Veremos los pasos a seguir para saber si una función es diferenciable en un punto.
Optimización de Funciones de Varias variables. Máximos relativos, mínimos relativos y puntos de silla de varias variables.
Dentro de este apartado Buscaremos:
máximos relativos , mínimos relativos y puntos de silla de 2 variables
máximos relativos, mínimos relativos y puntos de silla de 3 variables
máximos y mínimos restringidos en un entorno = máximos y mínimos absolutos de varias variables con 2 métodos:
Método de los Multiplicadores de Lagrange
Directamente trabajando sobre la región
En este apartado haremos dos ejercicios resueltos de como se aplica el Teorema de la Función Implícita para:
una función de varias variables
sistemas de ecuaciones o función vectorial
Polinomio de Taylor para Varias Variables
El polinomio de Taylor de orden 2 de una función de dos variables es:
En el video haremos el siguiente ejemplo:
Visita mi canal de YouTube: @ProfeInDaHouse